Definition 4.1 We say that a control ![]() is admissible with respect to the initial state vector
is admissible with respect to the initial state vector ![]() and
and ![]() ,
if
,
if
 |
(4.24) |
 |
(4.25) |
We impose the following assumptions on the process![]() and the cost function
and the cost function ![]() throughout this section.
throughout this section.
Assumption 4.5 Let ![]() for some integer
for some integer![]() ,
where
,
where ![]() .
The machine capacity process
.
The machine capacity process ![]() is a finite state Markov chain with the following infinitesimal generator
Q:
is a finite state Markov chain with the following infinitesimal generator
Q:
![\begin{displaymath}Qf({\mbox{\boldmath$m$ }})=\sum_{{\footnotesize\mbox{\boldm......({\mbox{\boldmath$m$ }}^{\prime })-f({\mbox{\boldmath$m$ }})]\end{displaymath}](img697.gif)
for some ![]() and any function
and any function ![]() on
on![]() .
Moreover, the Markov process is strongly irreducible and has the stationary
distribution
.
Moreover, the Markov process is strongly irreducible and has the stationary
distribution ![]() ,
,![]() .
.
Assumption 4.6 Let ![]() and
and![]() for
for ![]() .
Here pn represents the average capacity of the machine
n,
and n(i,j) is the number of machine placed on the
arc (i,j). Assume that there exist
.
Here pn represents the average capacity of the machine
n,
and n(i,j) is the number of machine placed on the
arc (i,j). Assume that there exist ![]() such that
such that
 |
(4.26) | ||
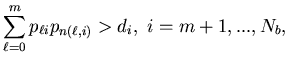 |
(4.27) |
 |
(4.28) |
| (4.29) |
Write (4.24) in the vector form
with ![]() .
Consider now the following equation:
.
Consider now the following equation:
 |
(4.30) |
Theorem 4.11 Assume
(i) ![]() with
with ![]()
![]() satisfies
(4.30); (ii) there exists
satisfies
(4.30); (ii) there exists![]() for
which
for
which
 |
(4.31) |
| (4.32) |
| = | ![$\displaystyle \inf_{{\footnotesize\mbox{\boldmath$u$ }}(\cdot )\in {\cal A}({\......ambda \right) dt+f({\mbox{\boldmath$x$ }}(T),{\mbox{\boldmath$m$ }}(T))\right]$](img661.gif) |
||
| = | ![$\displaystyle E\left[ \int_{0}^{T}\left( G({\mbox{\boldmath$x$ }}^{\ast }(t),{......ht) dt+f({\mbox{\boldmath$x$ }}^{\ast }(T),{\mbox{\boldmath$m$ }}(T))\right] .$](img662.gif) |
(4.33) |
Define the value function of the discounted cost problem as
Theorem 4.12 There exists
a sequence ![]() with
with ![]() as
as![]() such that for
such that for ![]() :
:
![\begin{eqnarray*}&&\lim_{k\rightarrow \infty }\rho _{k}V^{\rho _{k}}({\mbox{\b......m$ }}^{0})]=W({\mbox{\boldmath$x$ }},{\mbox{\boldmath$m$ }}),\end{eqnarray*}](img679.gif)
Theorem 4.13 (i) In our
problem, ![]() does not depend on
does not depend on ![]() ,
and
(ii) the pair
,
and
(ii) the pair![]() defined
in Theorem4.12 is a solution
to (4.19).
defined
in Theorem4.12 is a solution
to (4.19).
Remark 4.8 Assumption
4.6
is not needed in the discounted case. It is clear that this condition is
necessary for the finiteness of the long-run average cost in the case when ![]() tends to
tends to ![]() as
as ![]() .
Theorem 4.13 states in particular that
this condition is also sufficient.The proof of Theorems 4.12
and 4.13 is based on the following lemma
obtained in Presman, Sethi, and Zhang (1999b).
.
Theorem 4.13 states in particular that
this condition is also sufficient.The proof of Theorems 4.12
and 4.13 is based on the following lemma
obtained in Presman, Sethi, and Zhang (1999b).
Lemma 4.3 For any ![]() and
and![]() ,
there exists a control policy
,
there exists a control policy![]() such that for any
such that for any![]()
 |
(4.34) |
and ![]() is the surplus process corresponding to the control policy
is the surplus process corresponding to the control policy ![]() and the initial condition
and the initial condition ![]() .
.