

Next:5.4
Hierarchical controls of dynamicUp:5.
Hierarchical Controls under thePrevious:5.2
Hierarchical control of single
5.3 Hierarchical controls of dynamic flowshops
We are given a stochastic process on the standard probability space
on the standard probability space ,
where
,
where  is the capacity of the kth machine at time t, and
is the capacity of the kth machine at time t, and  is a small parameter to be specified later. We use
is a small parameter to be specified later. We use  to denote the input rate to the kth machine, k=1,...,N,
and
to denote the input rate to the kth machine, k=1,...,N,
and to denote the number of parts in the buffer between the kth and
(k+1)th machines, k=1,...,N-1. We assume a constant
demand rate z. The difference between cumulative production and
cumulative demand, called surplus, is denoted by
to denote the number of parts in the buffer between the kth and
(k+1)th machines, k=1,...,N-1. We assume a constant
demand rate z. The difference between cumulative production and
cumulative demand, called surplus, is denoted by  .
If
.
If ,
we have finished good inventories, and if
,
we have finished good inventories, and if  ,
we have a backlog.
,
we have a backlog.
The dynamics of the system can then be written as follows:

|
|
|
(5.21) |
where  and ak>0 are constants. The attrition rate ak
represents the deterioration rate of the inventory of the part type k
when
and ak>0 are constants. The attrition rate ak
represents the deterioration rate of the inventory of the part type k
when  (k=1,...,N-1), and it represents a rate of cancelation of
backlogged orders for finished goods when
(k=1,...,N-1), and it represents a rate of cancelation of
backlogged orders for finished goods when  .
We assume symmetric deterioration and cancelation rates for finished good
N
only for convenience in exposition. It would be easy to extend our results
if a+N>0 had denote the deterioration
rate and a-N>0 had denoted the order
cancelation rate.
.
We assume symmetric deterioration and cancelation rates for finished good
N
only for convenience in exposition. It would be easy to extend our results
if a+N>0 had denote the deterioration
rate and a-N>0 had denoted the order
cancelation rate.
Equation (5.21) can be written in the
following vector form:

|
|
|
(5.22) |
where A and B are given in Section 2.2,
and  .
Since the number of parts in the internal buffers cannot be negative, we
impose the state constraints
.
Since the number of parts in the internal buffers cannot be negative, we
impose the state constraints  ,
k=1,...,
N-1.
To formulate the problem precisely, let
,
k=1,...,
N-1.
To formulate the problem precisely, let  denote the state constraint domain, for
denote the state constraint domain, for  ,
let
,
let

|
|
|
(5.23) |
and for  let
Let the sigma algebra
let
Let the sigma algebra  .
We now define the concept of admissible controls.
.
We now define the concept of admissible controls.
Definition 5.5 We say that a
control  is admissible with respect to the initial state vector
is admissible with respect to the initial state vector if
if
-
(i)
-
 is an
is an  -adapted
measurable process;
-adapted
measurable process;
-
(ii)
-
 for all
for all ;
;
-
(iii)
-
the corresponding state process
 for all
for all .
.
The problem is to find an admissible control  that minimizes the cost function
that minimizes the cost function
![$\displaystyle J^{\varepsilon}({\mbox{\boldmath$x$ }}^0, {\mbox{\boldmath$m$ }}^......oldmath$x$ }}^{\varepsilon}(t))+u({\mbox{\boldmath$u$ }}^{\varepsilon}(t))]dt,$](img893.gif)
|
|
|
(5.25) |
where  defin[Aes the cost of inventory/shortage,
defin[Aes the cost of inventory/shortage, is the production cost, and
is the production cost, and  is the initial value of
is the initial value of  .
We impose the following assumptions on the random process
.
We impose the following assumptions on the random process and the cost function
and the cost function  and
and  throughout this section.
throughout this section.
Assumption 5.2 Let  for some given integer
for some given integer  ,
where
,
where  ,
withmjk,
k=1,...,N,
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process
,
withmjk,
k=1,...,N,
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process  is a finite state Markov chain with the infinitesimal generator
is a finite state Markov chain with the infinitesimal generator 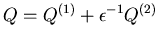 ,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that
,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that  if
if  ,
and
,
and for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies

Assumption 5.3 Assume that
Q(2) is weakly irreducible. Let  denote the equilibrium distribution of Q(2). That is,
denote the equilibrium distribution of Q(2). That is, is the only nonnegative solution to the equation
is the only nonnegative solution to the equation

|
|
|
(5.26) |
Furthermore, we assume that

|
|
|
(5.27) |
Assumption 5.4 and
and  are non-negative convex function. For all
are non-negative convex function. For all  and
and  ,
j=1,...,p,
there exist constants C and
,
j=1,...,p,
there exist constants C and  such that
such that

and
 We use
We use  to denote the set of all admissible controls with respect to
to denote the set of all admissible controls with respect to  and
and  .
Let
.
Let denote the minimal expected cost, i.e.,
denote the minimal expected cost, i.e.,

|
|
|
(5.28) |
We know, by Theorem 2.4 in [], that under Assumption 5.3, is independent of the initial condition
is independent of the initial condition  .
Thus we will use
.
Thus we will use  instead of
instead of .
We use
.
We use  to denote our control problem, i.e.,
to denote our control problem, i.e.,
 |
|
|
(5.29) |
As in Fleming and Zhang (1998), the positive
attrition rate  implies a uniform bound for
implies a uniform bound for  .
Next we examine elementary properties of the relative cost known also as
the potential function and obtain the limiting control problem as
.
Next we examine elementary properties of the relative cost known also as
the potential function and obtain the limiting control problem as  .
The HJBDD equation associated with the average-cost optimal control problem
in
.
The HJBDD equation associated with the average-cost optimal control problem
in  ,
as shown in Sethi, Zhang, and Zhang (1998),
takes the form
where
,
as shown in Sethi, Zhang, and Zhang (1998),
takes the form
where  is the potential function of the problem
is the potential function of the problem ,
, denotes the directional derivative of
denotes the directional derivative of  along the direction
along the direction  ,
and
,
and  for any function
for any function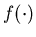 on
on  .
Moreover, following Presman, Sethi, and Zhang
(1999b), we can show that there exists a potential function
.
Moreover, following Presman, Sethi, and Zhang
(1999b), we can show that there exists a potential function such that the pair
such that the pair  is a solution of (5.30), where
is a solution of (5.30), where  is the minimum average expected cost for
is the minimum average expected cost for  .
.
The analysis of the problem begins with the boundedness of proved in Sethi, Zhang, and Zhang (1999a).
proved in Sethi, Zhang, and Zhang (1999a).
Theorem 5.7 The minimum
average expected cost  of
of  is
bounded in
is
bounded in ,
i.e.,
there exists a constant M1 >0
such that
,
i.e.,
there exists a constant M1 >0
such that

Next we derive the limiting control problem as  .
Intuitively, as the rates of the machine breakdown and repair approach
infinity, the problem
.
Intuitively, as the rates of the machine breakdown and repair approach
infinity, the problem  ,
which is termed the original problem, can be approximated by a simpler
problem called the limiting problem, where the stochastic machine
capacity process
,
which is termed the original problem, can be approximated by a simpler
problem called the limiting problem, where the stochastic machine
capacity process  is replaced by a weighted form. The limiting problem, which was first introduced
in Sethi, Zhang, and Zhou (1994), is formulated
as follows.
is replaced by a weighted form. The limiting problem, which was first introduced
in Sethi, Zhang, and Zhou (1994), is formulated
as follows.
As in Sethi and Zhang (1994c), we consider
the enlarged control space

such that  ,
for all
,
for all  ,
j=1,...,p,
and k=1,...,N, and the corresponding solution of the system
,
j=1,...,p,
and k=1,...,N, and the corresponding solution of the system
 satisfy
satisfy  for all
for all  .
Let
.
Let  represent the set of all these controls with
represent the set of all these controls with  .
The objective of this problem is to choose a control
.
The objective of this problem is to choose a control that minimizes
that minimizes
![\begin{displaymath}J( U(\cdot))=\limsup_{T \rightarrow \infty} \frac {1} {T} \......(s))+\sum_{j=0} ^p\gamma_j c({\mbox{\boldmath$u$ }}^j(s))]ds.\end{displaymath}](img922.gif)
We use  to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem
to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem  as follows:
as follows:

The average cost optimality equation associated with the limiting control
problem  is
is

|
|
|
(5.31) |
where  is a potential function for
is a potential function for  and
and is the directional derivative of
is the directional derivative of along the direction
along the direction with
with .
From Presman, Sethi, and Zhang (1999a), we
know that there exist
.
From Presman, Sethi, and Zhang (1999a), we
know that there exist  and
and  such that (5.31) holds. Moreover,
such that (5.31) holds. Moreover,  is the limit of
is the limit of  as
as  .
Hierarchical controls are based on the convergence of the minimum average
expected cost
.
Hierarchical controls are based on the convergence of the minimum average
expected cost  as
as goes to zero. Thus we will consider the convergence, as well as the rate
of convergence. To do this, we first give without proof the following lemma
similar to Lemma C.3 of Sethi and Zhang (1994a)].
goes to zero. Thus we will consider the convergence, as well as the rate
of convergence. To do this, we first give without proof the following lemma
similar to Lemma C.3 of Sethi and Zhang (1994a)].
Lemma 5.4 Let

Then, for any bounded deterministic measurable process ,
, ,
and
,
and ,
which
is a Markov time with respect to
,
which
is a Markov time with respect to  ,
there
exists positive constants C and
,
there
exists positive constants C and  such that
such that
 for all
for all and
sufficiently small
and
sufficiently small .
.
In order to get the required convergence result, we need the following
auxiliary result, which is the key to obtaining the convergence result.
Lemma 5.5 For  and
any sufficiently small
and
any sufficiently small ,
there
exist C>0,
,
there
exist C>0,  and
and
 such that for each j=1,...,N
such that for each j=1,...,N

|
|
|
(5.32) |
and
![$\displaystyle \lambda +C_{59} \varepsilon^{\delta}>\limsup_{T \rightarrow \inf......))+\sum_{i=1}^p\gamma_i c({\mbox{\boldmath$u$ }}^i(\varepsilon, t))\right]dt,$](img940.gif)
|
|
|
(5.33) |
where  is the trajectory under
is the trajectory under 
For the proof, see Sethi, Zhang, and Zhang
(1999a). With the help of Lemma 5.5,
Sethi,
Zhang, and Zhang (1999a) give the following lemma.
Lemma 5.6 For  ,
there exist
,
there exist ,
, ,
,  ,
and
,
and
 such that
such that

|
|
|
(5.34) |
and
![$\displaystyle \lambda +\hat C_{52} \varepsilon^{\delta}>\limsup_{T \rightarrow......t))+\sum_{i=1}^p\gamma_i c({\mbox{\boldmath$u$ }}^i(\varepsilon, t))\right]dt,$](img947.gif)
|
|
|
(5.35) |
where  is the state trajectory under the control
is the state trajectory under the control  .
.
With Lemmas 5.4, 5.5
and
5.6, we can state the main result
of this section proved in Sethi, Zhang, and
Zhang (1999a).
Theorem 5.8 For any  ,
there exists a constant
,
there exists a constant  such that for all sufficiently small
such that for all sufficiently small ,
,

|
|
|
(5.36) |
This implies in particular that 
Finally we give the procedure to construct an asymptotic optimal control.
Construction of an Asymptotic Optimal Control
Step I: Pick an  -optimal
control
-optimal
control for
for  ,
i.e.,
,
i.e.,
![\begin{eqnarray*}\limsup_{T \rightarrow \infty}\frac{1}{T}\int^T_0 [h(x(t))+......amma_j c({\mbox{\boldmath$u$ }}^j(t))]dt<\lambda+\varepsilon.\end{eqnarray*}](img954.gif) Let
Let

Furthermore, let
 and
and

Define
 Then we get the control
Then we get the control

This step can be called partial pathwise lifting.
Step II: Define

Then we get the control

This step can be called pathwise shrinking.
Step III: We choose

such that

This step can be called entire pathwise lifting.
Step IV: Set
 and
and
 Set
Set

Sub-step n(n=2,...,N): Set



 Then we get
Then we get  .
.


Next:5.4
Hierarchical controls of dynamicUp:5.
Hierarchical Controls under thePrevious:5.2
Hierarchical control of single
![]() is admissible with respect to the initial state vector
is admissible with respect to the initial state vector![]() if
if
![$\displaystyle J^{\varepsilon}({\mbox{\boldmath$x$ }}^0, {\mbox{\boldmath$m$ }}^......oldmath$x$ }}^{\varepsilon}(t))+u({\mbox{\boldmath$u$ }}^{\varepsilon}(t))]dt,$](img893.gif)
![]() for some given integer
for some given integer ![]() ,
where
,
where ![]() ,
withmjk,
k=1,...,N,
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process
,
withmjk,
k=1,...,N,
denoting the capacity of the kth machine,
j=1,...,p.
The capacity process ![]() is a finite state Markov chain with the infinitesimal generator
is a finite state Markov chain with the infinitesimal generator ![]() ,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that
,
whereQ(1)=(qij(1))
and Q(2)=(qij(2))
are matrices such that ![]() if
if ![]() ,
and
,
and![]() for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
for r=1,2. Moreover,
Q(2) is irreducible and,
without any loss of generality, it is taken to be the one that satisfies
![]() denote the equilibrium distribution of Q(2). That is,
denote the equilibrium distribution of Q(2). That is,![]() is the only nonnegative solution to the equation
is the only nonnegative solution to the equation





![]() proved in Sethi, Zhang, and Zhang (1999a).
proved in Sethi, Zhang, and Zhang (1999a).
![]() of
of ![]() is
bounded in
is
bounded in![]() ,
i.e.,
there exists a constant M1 >0
such that
,
i.e.,
there exists a constant M1 >0
such that
![]() .
Intuitively, as the rates of the machine breakdown and repair approach
infinity, the problem
.
Intuitively, as the rates of the machine breakdown and repair approach
infinity, the problem ![]() ,
which is termed the original problem, can be approximated by a simpler
problem called the limiting problem, where the stochastic machine
capacity process
,
which is termed the original problem, can be approximated by a simpler
problem called the limiting problem, where the stochastic machine
capacity process ![]() is replaced by a weighted form. The limiting problem, which was first introduced
in Sethi, Zhang, and Zhou (1994), is formulated
as follows.
is replaced by a weighted form. The limiting problem, which was first introduced
in Sethi, Zhang, and Zhou (1994), is formulated
as follows.
![]() ,
for all
,
for all ![]() ,
j=1,...,p,
and k=1,...,N, and the corresponding solution of the system
,
j=1,...,p,
and k=1,...,N, and the corresponding solution of the system

![\begin{displaymath}J( U(\cdot))=\limsup_{T \rightarrow \infty} \frac {1} {T} \......(s))+\sum_{j=0} ^p\gamma_j c({\mbox{\boldmath$u$ }}^j(s))]ds.\end{displaymath}](img922.gif)
![]() to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem
to denote the above problem, and will regard this as our limiting problem.
Then we define the limiting control problem ![]() as follows:
as follows:

![]() is
is

![]() ,
,![]() ,
and
,
and![]() ,
which
is a Markov time with respect to
,
which
is a Markov time with respect to ![]() ,
there
exists positive constants C and
,
there
exists positive constants C and ![]() such that
such that
![]() and
any sufficiently small
and
any sufficiently small![]() ,
there
exist C>0,
,
there
exist C>0, ![]() and
and


![$\displaystyle \lambda +C_{59} \varepsilon^{\delta}>\limsup_{T \rightarrow \inf......))+\sum_{i=1}^p\gamma_i c({\mbox{\boldmath$u$ }}^i(\varepsilon, t))\right]dt,$](img940.gif)
![]() ,
there exist
,
there exist![]() ,
,![]() ,
, ![]() ,
and
,
and

![$\displaystyle \lambda +\hat C_{52} \varepsilon^{\delta}>\limsup_{T \rightarrow......t))+\sum_{i=1}^p\gamma_i c({\mbox{\boldmath$u$ }}^i(\varepsilon, t))\right]dt,$](img947.gif)
![]() ,
there exists a constant
,
there exists a constant ![]() such that for all sufficiently small
such that for all sufficiently small![]() ,
,
![]() -optimal
control
-optimal
control![]() for
for ![]() ,
i.e.,
,
i.e.,
![\begin{eqnarray*}\limsup_{T \rightarrow \infty}\frac{1}{T}\int^T_0 [h(x(t))+......amma_j c({\mbox{\boldmath$u$ }}^j(t))]dt<\lambda+\varepsilon.\end{eqnarray*}](img954.gif)






